Egy textilgyár felmérést készített, hogy a vásárlói igényeknek megfelelő arányban gyárthassa le törölközőit. Megkérdeztek 500 járókelőt arról, hogy négy lehetséges szín közül melyik színben vásárolnának legszívesebben ilyen törölközőt. Az alábbi táblázatban látható a felmérés eredménye.
| kék | sárga | piros | zöld | |
| válaszok száma | 176 | 153 | 124 | 47 |
A gyár a válaszoknak megfelelő arányban határozta meg az egyes színekből készülő törölközők darabszámát.
a) Számítsa ki, hogy hány kék, sárga, piros, illetve zöld törölközőt gyártottak, ha összesen 10 000 darab készült! A darabszámokat százasokra kerekítve adja meg!
Négy kék, két sárga és egy piros törölköző közül (visszatevés nélkül) véletlenszerűen kiválasztunk kettőt.
b) Mennyi annak a valószínűsége, hogy mindkét törölköző sárga lesz?
A textilgyárban dolgozók között tavaly háromszor annyi nő volt, mint férfi. Idén felvettek még 70 nőt és 6 férfit, így már négyszer annyi nő dolgozik a gyárban, mint férfi.
c) Hány nő és hány férfi dolgozója van a gyárnak idén?
Kóstolóval egybekötött termékbemutatót tartottak egy új kávékeverék piaci megjelenését megelőzően. Két csoport véleményét kérték úgy, hogy a terméket az 1-től 10-ig terjedő skálán mindenkinek egy-egy egész számmal kellett értékelnie. Mindkét csoport létszáma 20 fő volt. A csoportok értékelése az alábbi táblázatban látható.
| pontszám | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| gyakoriság az 1. csoportban | 0 | 0 | 1 | 0 | 6 | 8 | 2 | 2 | 1 | 0 |
| gyakoriság az 1. csoportban | 0 | 8 | 0 | 2 | 0 | 1 | 0 | 0 | 0 | 9 |
a) Ábrázolja közös oszlopdiagramon, különböző jelölésű oszlopokkal a két csoport pontszámait! A diagramok alapján fogalmazzon meg véleményt arra vonatkozóan, hogy melyik csoportban volt nagyobb a pontszámok szórása! Véleményét a diagramok alapján indokolja is!
b) Hasonlítsa össze a két csoport pontszámainak szórását számítások segítségével is!
Kétféle kávéból 14 kg 4600 Ft/kg egységárú kávékeveréket állítanak elő. Az olcsóbb kávéfajta egységára 4500 Ft/kg, a drágábbé pedig 5000 Ft/kg. darab
c) Hány kilogramm szükséges az egyik, illetve a másik fajta kávéból?
Az ábrán egy kis múzeum alaprajzát látjuk. A múzeum termei közötti kapcsolatot gráffal is szemléltethetjük.
A gráf pontjai a termek, élei pedig az átjárók a termek között. (Egy él egy átjárót szemléltet két terem között.)

a) Rajzolja fel a múzeum termeit és átjáróit szemléltető gráfot!
A múzeumba háromféle belépőjegyet lehet váltani:
| Teljes árú jegy | 400 Ft |
| Kedvezményes jegy (gyerek, diák, pedagógus, nyugdíjas) | 250 Ft |
| Fotójegy (belépőjegy és fényképezőgép-használat) | 500 Ft |
Januárban négyszer annyi kedvezményes belépőjegyet adtak el, mint teljes árú jegyet, továbbá az eladott fotójegyek száma az eladott teljes árú jegyek számának 12,5%-a volt.
A múzeum belépőjegy-eladásból származó bevétele januárban 912 600 Ft volt.
b) Hány belépőjegyet adtak el januárban összesen?
Csilla, Dezső, Emese, Feri és Gyöngyi délelőtt 10-re beszéltek meg találkozót a múzeum előtt. Sorban egymás után érkeznek (különböző időpontokban), véletlenszerűen.
c) Mennyi a valószínűsége annak, hogy legfeljebb egy lánynak kell várakoznia fiúra?
A kiállításon több gondolkodtató, minimalista kép is szerepel. Dezső szerint az ábrán látható, csatlakozó félköröket ábrázoló kép címe azért „Egyenlőség”, mert a felső és az alsó görbe vonal
hossza egyenlő. A felső görbét alkotó két egyforma félkör átmérőjének összege 48 cm. Az alsó görbét alkotó két félkör átmérőjének összege szintén 48 cm.

d) Igaz-e Dezső sejtése, hogy a két görbe vonal hossza egyenlő?








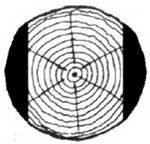 A Hód Kft. faárutelephelyén rönkfából (henger alakú fatörzsekből) a következő módon készítenek gerendát. A keretfűrészgép először két oldalt levág egy-egy – az ábrán sötéttel jelölt – részt, majd a fa 90°-kal történő elfordítása után egy hasonló vágással végül egy négyzetes hasáb alakú gerendát készít.
A Hód Kft. faárutelephelyén rönkfából (henger alakú fatörzsekből) a következő módon készítenek gerendát. A keretfűrészgép először két oldalt levág egy-egy – az ábrán sötéttel jelölt – részt, majd a fa 90°-kal történő elfordítása után egy hasonló vágással végül egy négyzetes hasáb alakú gerendát készít. 







