Egy felül nyitott doboz vízszintes asztallapon áll. A dobozt három téglalap és két derékszögű trapéz határolja.
A doboznak a vízszintes síkra illeszkedő lapja 8 cm × 6 cm méretű, két egymással szemközti függőleges síkú lapja pedig 6 cm × 5 cm, illetve 6 cm × 2 cm méretű téglalap.

a) Számítsa ki a doboz testátlóinak hosszát!
A test kiterített hálóját az ábra sötétített tartománya szemlélteti. Ezt a hálót egy 15 cm × 16 cm-es téglalapból vágjuk ki (ennek oldalai párhuzamosak a test 8 cm × 6 cm-es alaplapjának oldalaival).

c) Mekkorának válasszuk a kartonlap oldalainak hosszát, hogy a területe a lehető legkisebb legyen?
Egy felül nyitott doboz vízszintes asztallapon áll. A dobozt három téglalap és két derékszögű trapéz határolja.
A doboznak a vízszintes síkra illeszkedő lapja 8 cm × 6 cm méretű, két egymással szemközti függőleges síkú lapja pedig 6 cm × 5 cm, illetve 6 cm × 2 cm méretű téglalap.

a) Számítsa ki a doboz testátlóinak hosszát!
A test a 6 cm-es él felezőpontján átmenő függőleges síkra szimmetrikus, ezért) csak kétféle hosszúságú testátló van.
A D1 rövidebb testátló hossza egy 6 × 8 × 2 cm élű téglatest testátlója:
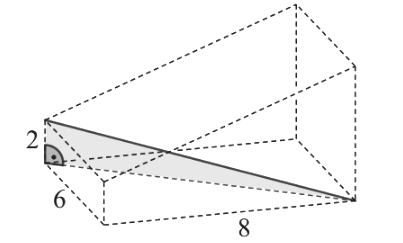
A D2 hosszabb testátló hossza egy 6 × 8 × 5 cm élű téglatest testátlója:
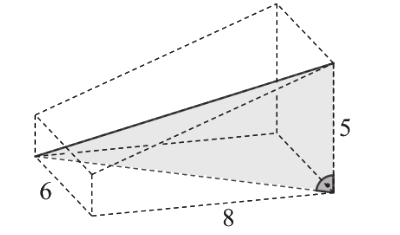
A test kiterített hálóját az ábra sötétített tartománya szemlélteti. Ezt a hálót egy 15 cm × 16 cm-es téglalapból vágjuk ki (ennek oldalai párhuzamosak a test 8 cm × 6 cm-es alaplapjának oldalaival).
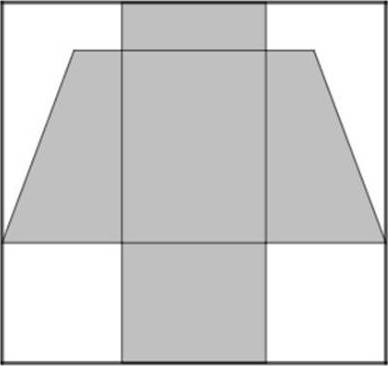
b) Hány százalék hulladék keletkezik?
A téglalap területe, amelyből a test hálója kivágható:
A hulladék területe összesen:
Egy téglalap alakú kartonlap oldalhosszait úgy szeretnénk megválasztani, hogy alul és felül 4-4 cm-es, jobb és bal oldalon 2-2 cm-es margót hagyva a lap közepén megmaradó téglalap alakú terület 50 cm2 nagyságú legyen.

c) Mekkorának válasszuk a kartonlap oldalainak hosszát, hogy a területe a lehető legkisebb legyen?
A kartonlap területe a lap közepén megmaradó téglalap szélességének (x) függvényében:
Ennek a függvénynek ott lehet minimuma, ahol az első deriváltja 0.
A feladat természetéből adódóan csak a pozitív (egy téglalap oldalának szélessége csak pozitív szám lehet) eredménynek van értelme.
Vizzsgáljuk meg, vajon az x=5 értékben a függvénynek minimuma vagy maximuma van. Ezt a második derivált előjelével tehetjük meg.
A függvénynek ezért az x=5 értékben (lokális és egyben abszolút) minimumhelye van.
A kartonlap szélessége:
A kartonlap magassága:
A kartonlap méretei centiméterben:





