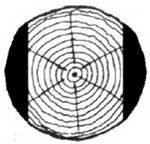
A Hód Kft. faárutelephelyén rönkfából (henger alakú fatörzsekből) a következő módon készítenek gerendát. A keretfűrészgép először két oldalt levág egy-egy – az ábrán sötéttel jelölt – részt, majd a fa 90°-kal történő elfordítása után egy hasonló vágással végül egy négyzetes hasáb alakú gerendát készít.
A gépet úgy állítják be, hogy a kapott hasáb alaplapja a lehető legnagyobb legyen.  Most egy forgáshenger alakú, 60 cm átmérőjű, 5 méter hosszú rönkfát fűrészel így a gép.

a) Igaz-e, hogy a kapott négyzetes hasáb alakú fagerenda térfogata kisebb 1 köbméternél?

A Hód Kft. deszkaárut is gyárt, ehhez a faanyagot 30 000 Ft/m3-es beszerzési áron vásárolja meg a termelőtől. A gyártás közben a megvásárolt fa kb. 40%-ából hulladékfa lesz. A késztermék 1 köbméterét 90 000 forintért adja el a cég, de az eladási ár 35%-át a költségekre kell fordítania (feldolgozás, telephely fenntartása stb.)

b) Mennyi haszna keletkezik a Hód Kft.-nek 1 köbméter deszkaáru eladásakor?

A fakitermelő cég telephelyéről hat teherautó indul el egymás után. Négy teherautó fenyőfát, kettő pedig tölgyfát szállít.

c) Számítsa ki annak a valószínűségét, hogy a két, tölgyfát szállító teherautó közvetlenül egymás után gördül ki a telephelyről, ha az autók indulási sorrendje véletlenszerű!