Másodfokú egyenlet

a x^{2} + b x + c = 0

Az egyenlet megoldásai, vagy más néven gyökei, nullái:

x_{1, 2} = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}

Göktényezős alak:

a x^{2} + b x + c = a (x - x_{1}) (x - x_{2})

Viète-formulák:

x_{1} + x_{2} = - \frac{b}{a}; x_{1} \cdot x_{2} = \frac{c}{a}

Diszkrimináns:

D = b^{2} - 4 a c

$D > 0 \Rightarrow x_{1}, x_{2} \in ℝ$	a gyökök különbözőek és valósak
$D = 0 \Rightarrow x_{1} = x_{2} \in ℝ$	egy valós gyök van
$D < 0 \Rightarrow x_{1} = \bar{x_{2}} \in ℂ$	nics valós gyök (a gyökök konjugált komplex számok)

A másodfokú egyenlet mint függvény

y = a x^{2} + b x + c

A másodfokú függvény grafikonja

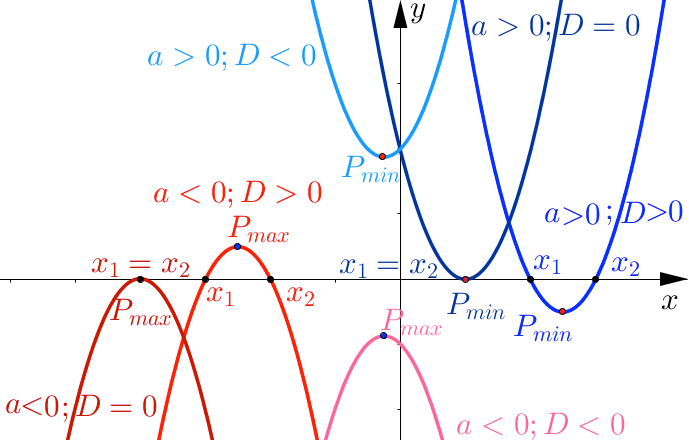
A parabola P csúcspontjának koordinátái:

P (- \frac{b}{2 a}, - \frac{b^{2} - 4 a c}{4 a})

Kulcsszavak:

Polinómok
Binóm négyzete és köbe, négyzetek különbsége, köbök különbsége és összege
Sorozatok
Számtani sorozat
Mértani sorozat
Logaritmus
Logaritmus
Kapcsolat különböző alapú logaritmusok között
Hatványozás
Hatványozás foglama és azonosságai
Gyökvonás
Gyökvonás foglama és azonosságai
Arányosság
Egyenes és fordított arányosság
Egyenlőtlenségek
Egyenlőtlenségek
Egyenletek
Másodfokú egyenlet
Harmadfokú egyenlet
Irracionális és transzcendens egyenletek
Komplex számok
Komplex számok
Komplex számok összeadása - kivonása
Komplex számok szorzása - osztása
Komplex számok hatványozása
Komplex számok gyökvonása
Katamtszámítás
Kamatszámítás
Mátrixok
Mátrixok definiciója, összeadása, kivonása
Mátrixok szorzása