Vector Product of Vectors

\vec{a} = x_{1} \vec{i} + y_{1} \vec{j} + z_{1} \vec{k}

\vec{b} = x_{2} \vec{i} + y_{2} \vec{j} + z_{2} \vec{k}

\vec{c} ⊥ \vec{a} \land \vec{c} ⊥ \vec{b}

\vec{c} = \vec{a} \times \vec{b} = | \begin{matrix} \vec{i} & \vec{j} & \vec{k} \\ x_{1} & y_{1} & z_{1} \\ x_{2} & y_{2} & z_{2} \end{matrix} |

\vec{c} = (y_{1} z_{2} - z_{1} y_{2}) \vec{i} + (z_{1} x_{2} - x_{1} z_{2}) \vec{j} + (x_{1} y_{2} - y_{1} x_{2}) \vec{k}

| \vec{c} | = | \vec{a} | \cdot | \vec{b} | \cdot s i n α

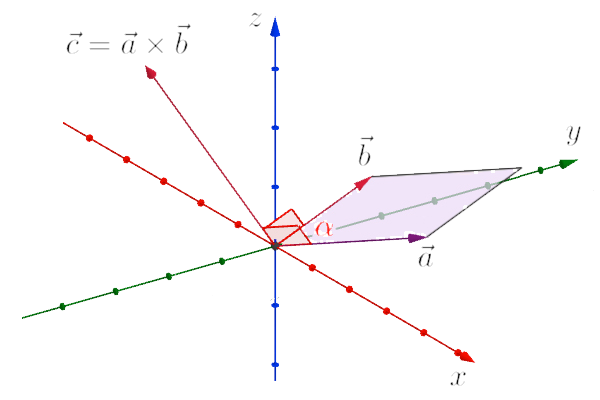
The result of vector product, vector $\vec{c}$ , has a length that is equal with the area of parallelogram between vecrors $\vec{a}$ and $\vec{b}$ (pink area).

Keywords: multiplication of vectors, vector product

Trigonometry
Law of Sines
Law of Cosines
Trigonometric identities of double angles
Trygonometry Identities of same angle
Trigonometric identities of half angles
Identities for the sum and difference of two angles
Sum and difference of trigonometric functions
Trigonometric Values of Special Angles
Two-dimensional geometric shapes
Angle Bisector Theorem
The inscribed angle theorem
Convex - Concave polygons, functions
Regular and Irregular Polygons
Thales Theorem
Triangle
Special Triangles - Right Triangle, Equilateral Triangles, Isosceles Triangles
Quadrilateral
Squere
Rectangle
Rhombus
Parallelogram
Kite
Trapezoid
Circle
Circular sector
Circular segment
Three-dimensional geometric shapes
Cube
Sphere
Cone
Prism
Pyramide
Platonic solids
Cylinder
Vectors
Scalar Product of Vectors
Vector Product of Vectors
Analytical Geometry 2D
Distance between two points
Circle
Hyperbole
Linear equation
Parabola
Ellipse
Analytical Geometry 3D
Plane