760/HK19. példa / Matematika - Megoldott feladatok gyűjteménye

MR-760 / 15. példa

Az ABCD négyzet oldalának hossza 12 egység. A négyzet belsejében kijelöltük az E pontot úgy, hogy BE = CE = 12 egység legyen (lásd az ábrát).

a) Számítsa ki az A és E pontok távolságát!

Egy bronzból készült, szabályos négyoldalú gúla alakú tömör test (piramis) minden éle 10 cm hosszúságú.

b) Számítsa ki a gúla tömegét, ha 1 dm³ bronz tömege 8 kg!

Forrás: Magyarország: Közép szintű matematika érettségi [2019. május 7.] - 15..)

Geometria → Síkidomok → Négyszög

a) Számítsa ki az A és E pontok távolságát!

Az ABE háromszögre alkalmazhatjuk a koszinusztételt:

${\bar{A E}}^{2} = 12^{2} + 12^{2} - 2 \cdot 12 \cdot 12 \cdot \cos 30 °$

${\bar{A E}}^{2} \approx 38, 58$

Egy bronzból készült, szabályos négyoldalú gúla alakú tömör test (piramis) minden éle 10 cm hosszúságú.

b) Számítsa ki a gúla tömegét, ha 1 dm³ bronz tömege 8 kg!

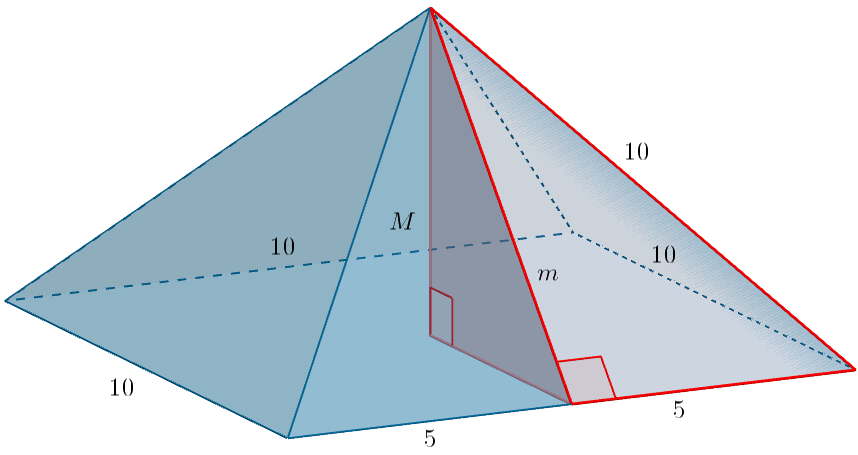
A gúla oldallapjának magassága Pitagorasz-tétellel:

$10^{2} = m^{2} + 5^{2}$

$m^{2} = 10^{2} - 5^{2}$

$m^{2} = 100 - 25$

$m^{2} = 75$

$m = \sqrt{75}$

A gúla magassága Pitagorasz-tétellel:

$m^{2} = 5^{2} + M^{2}$

$75 = 25 + M^{2}$

$M^{2} = 75 - 25$

$M^{2} = 50$

$M = \sqrt{50}$

$V = \frac{a^{2} \cdot M}{3}$

$V = \frac{10^{2} \cdot \sqrt{50}}{3}$

$V \approx 235, 7 c m^{3}$

$1 d m^{3} = 10 c m \cdot 10 c m \cdot 10 c m = 1000 c m^{3}$

$V \approx 235, 7 c m^{3} = 0, 2357 d m^{3}$

A gúla tömege ez alapján:

$x \approx 8 \cdot 0, 2357$

$x \approx 1, 89 k g$