Platonic solids
Step-by-step by clicking
Played automatically
Showing all
Just the solution
What do I need to know?
Name
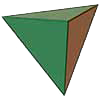
Tetraedron
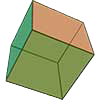
Hexahedron (Cube)
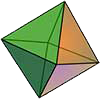
Octahedron
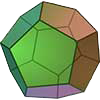
Dodecahedron
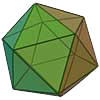
Icosahedron
Kép
Háló
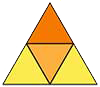
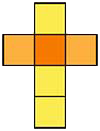
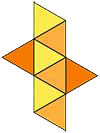
Faces
4
6
8
12
20
Face type
equilateral triangle
squere
equilateral triangle
equilateral triangle
equilateral triangle
Duality
tetrahedron
octahedron
hexahedron
icosahedron
dodecahedron
Edges
6
12
12
30
30
Vertices
4
8
6
20
12
Edges from vertex
3
3
4
3
5
Number of diagonals
0
4
3
100
36
Dihedral angle
≈70°31'44''
90°
≈109°28'16''
≈116°33'56''
≈138°11'23''
Surface area
Volume
Circumradiu
Inradiu
Midradius
Keywords: Platonic solids, also called the regular solids or regular polyhedra